Bir yerin koordinat mevkini ölçmek; o yerin Dünya koordinat
sistemine göre enlem ve boylam değerini belirlemektir.
Su ile kaplanmış hali ile Dünyamız kutuplardan hafif basık
“Elipsoit” biçimdedir. Ancak Dünya’nın kutuplardan bu basıklığı denizcilik
açısından ihmal edilebilir bir değerde olup koordinat sisteminde Dünya tam bir
küre olarak ele alınmaktadır.
Dünya,
merkezinden geçen bir eksen etrafında döner. Bu eksen yeryüzünü iki noktada
keser. Bu noktalardan biri bizim “Kuzey Kutbu” olarak belirttiğimiz nokta,
diğeri de “Güney Kutbu” olarak belirttiğimiz noktadır.
Her bir kutuptan ayrı ayrı olarak yeryüzündeki eşit
uzaklıktaki noktaların geometrik yerine enlem (paralel, arz) denir. Dünya’nın
kutuplarını yeryüzünde en kısa yoldan birleştiren hatlara da boylam (meridyen,
tûl) denir. Dünya koordinat sistemi bu enlem ve boylam dediğimiz yeryüzünü
dilimleyen hayali referans çizgilerden oluşmuştur.
Yeryüzünde her iki kutuptan eşit uzaklıktaki
noktaların geometrik yeri, Dünya’yı tam ortasından çevreleyen çember olup buna
“Ekvator” denir. Ekvator, enlemlerin isimlendirilmesinde referanstır. Bir
enlemin ismi; o enlemin Dünya merkezine göre ekvator ile arasındaki açısal
uzaklıktır. Şekilden de görülebileceği üzere bu açı en fazla 90 derecedir. Bir
başka deyişle ekvatorun kuzeyinde ve güneyinde 90’ar tane tam derecelik enlem
vardır. Bu isimlendirme açı değeri ve sonuna konulan yakın kutup simgesi ile
yapılır.
Örnek:
Ekvatorun kuzeyinde ekvator ile arasında Dünya
merkezinden 42 derecelik açısal fark olan “X” noktasının enlemi (420N)
şeklinde isimlendirilir ve gösterilir. (0) İşareti dereceyi, (N)
işareti “kuzey” kelimesinin İngilizce karşılığı olan (North) kelimesini ifade
eder.
Örnek:
Ekvatorun güneyinde, ekvator ile arasında Dünya
merkezinden 5 derecelik açısal fark olan enlem (050S) şeklinde
isimlendirilir ve gösterilir. (S) işareti “güney” kelimesinin İngilizce
karşılığı olan (South) kelimesini ifade etmektedir.
Enlem tam dereceleri kuzey ve güney yarım kürelerinde
en fazla 90’ar adet olduğundan bildirimlerde yanlış anlaşılmayı engellemek
maksadı ile enlemler iki basamaklı olarak ifade edilirler. Bu neden ile “5”in
başına bir tane “0” konulmuştur.
Boylamların ölçülmesinde ve isimlendirilmesinde de
İngiltere’nin Greenwich rasathanesinden geçen boylam referans olarak
alınmıştır. Bu boylam sıfır derece boylamıdır. Diğer boylamlar, Dünya dönüş
ekseninde “0” derece boylamı ile yaptıkları açısal farka göre
isimlendirilirler. Bu isimlendirme; açı değeri ve sonuna konulan taraf (doğu
veya batı) simgesinin belirtilmesi şekli ile yapılır.
Örnek:
Dünya eksenine göre “0” derece boylamının batı
tarafta, arasında 71 derecelik açısal fark olan boylam (0710 W)
şeklinde olarak isimlendirilir ve gösterilir. (W) İşareti “batı” kelimesinin
İngilizce karşılığı olan (West) kelimesini ifade etmektedir.
Referans boylamdan doğu ve batı yönüne en fazla
180’er adet tam derece boylamı olduğundan yanlış anlaşılmayı engellemek amacı
ile boylam dereceleri üç haneli olarak ifade edilirler. Tek basamaklı boylam
dereceleri ifade edilirken başına çift sıfır, çift basamaklı boylam dereceleri
ifade edilirken başına tek sıfır konur. Yukarıdaki örnekte de bu amaç ile 710’nin
önüne tek sıfır konmuştur.
Örnek:
Sıfır derece boylamının doğusunda, sıfır derece
boylamı ile dünya eksenine göre arasında 5 derecelik açısal fark olan boylam
(0050E) olarak ifade edilir. (E) işareti “doğu” kelimesinin
İngilizce karşılığı olan (East) kelimesini ifade temektedir.
Denizcilerin
denizlerde seyir yapabilmeleri için onlara denizleri ve kıyıları gösteren bir
yardımcıya ihtiyaçları vardır. Deniz seyir haritaları bu amaçla hazırlanmış
yardımcılar olup üzerlerindeki unsurlar ile yeryüzünün belirli bir bölümündeki
denizleri ve kıyıları gösteren, üzerine mevki konulabilen, mesafe ölçülebilen
ve rota çizilebilen haritalardır.
Dünya küre biçiminde
olduğundan Dünya’yı simgeleyen bir küre üzerinde yeryüzünün genel coğrafik
şekilleri gösterilebilir. Ancak gemilerde kullanılabilecek bir küre gerçeğe
göre çok küçük olacağından tüm teferruatlar bunun üzerinde gösterilemez ve
gösterilebilse bile küre şekli ile üzerinde seyir çalışması yapılamaz. Üzerinde
seyir çalışmasının yapılabilmesi için de her şeyden önce yeryüzü şeklilerinin
iki boyutlu bir görüntüsüne ihtiyaç vardır. İşte seyir haritaları küre
üzerindeki yeryüzü şekillerinin projeksiyon izdüşüm yöntemi ile iki boyutlu
hale getirilmesi ile oluşturulmuşlardır.
Harita çiziminde
kullanılan projeksiyon izdüşüm yöntemi; bir benzetme olarak dünya küresinin
merkezinde[1] bulunan bir ışık kaynağından çıkan ışınların yerkürenin dışında
ona teğet olan bir düzlem üzerinde oluşturduğu izden yararlanarak harita çizme
yöntemidir.
İzdüşüm yöntemleri
kullanılan düzlemlerin biçimine göre isimlendirilir. Bu farklı yöntemler ile
oluşturulan haritaların kullanım yer ve usulleri de çiziminde kullanılan
yöntemin özelliklerine göre belirlenir. Tüm izdüşüm yöntemlerinde teğet
noktasının yakınlarındaki görüntüler gerçeğe yakın ölçülerdeyken, uzaklaştıkça
şekilleri büyür ve değişir.
Silindirik izdüşüm
yöntemi; bir benzetme ile dünya küresinin merkezinde bulunan bir ışık
kaynağından çıkan ışınların yerküreye teğet olan bir silindir üzerinde
oluşturduğu izden yararlanarak bir harita çizme yöntemidir. Ekvatordan teğet
silindirik izdüşüm yöntemi ile yapılan bu haritalara Merkator (Mercator)
haritaları denir.
İzdüşüm yöntemlerinde
küre şeklinden iki boyutluya geçişte haritalarda bazı değişimler olur. Bu
değişimler bilinmeli ve harita ona göre kullanılmalıdır.
Merkator haritalarında
aşağıdaki değişimler meydana gelir.
● Gerçekte boylamlar kutuplara gittikçe bir birine
yaklaşmakta olmasına rağmen, Merkator haritasında boylamlar birleşmez ve bir
birine paralel durumda kalır.
● Gerçekte enlemlerin arası eşit olmasına rağmen,
Merkator haritasında kutuplara gittikçe, enlemlerin arası açılır.
Haritaların;
yeryüzündeki tüm yerlerin bir küreye işlenmesi ve sonra izdüşüm ile haritanın
oluşturulması yöntemi bugün artık yerini uydu fotoğrafları ile yapılan
haritalara bırakmıştır. Ancak bunlarda merkator projeksiyon sistemine uygun
haritalar olduğundan kullanımları değişmez.
Deniz seyir haritaları
üzerlerinde çizim çalışmalarının yapılabileceği büyüklüktedir. Kâğıdı defalarca
çizilip, silinmeye dayanıklı, rutubetten veya sıcaktan deforme olmayan cinsten
seçilir.
Özel haritalar hariç
deniz seyir haritaları yaklaşık olarak 70x105cm ebatlarındadır. Kâğıdın
kenarında 3 cm kalınlığında bir çerçeve bırakılır.
Harita bu çerçevenin 1 cm içerisinden enlem ve boylam
cetvelleri ile sınırlanmış şekilde basılır. Harita ister kuzey yarımküreye ister
güney yarımküreye ait olsun daima üst kenarı kuzey, alt kenarı güney, sağ
kenarı doğu, sol kenarı batı tarafıdır.
Haritanın sağ ve sol
kenarlarında üzerindeki her hangi bir noktanın enlemini bulmamıza yarayan
taksimatlı enlem cetvelleri, alt ve üst kanarlarında ise o noktanın boylam
değerini bulmamıza yarayan taksimatlı boylam cetvelleri bulunur. Tam dereceler
ile beşer aralıklı olarak dakikalar rakam ile cetvel üzerinde belirtilirken ara
değerler taksimatına göre hesaplanır. Ancak bu ifade genel olup çok büyük veya
çok küçük ölçekli haritalarda farklı durumlar ile karşılaşabiliriz.
Merkator haritalarının
özelliğine göre harita üzerinde enlemler ve boylamlar ayrı ayrı kendi
aralarında paralel, birbirleri ile de dik durumda çizgi ile belirtilirler. Normalde
sadece haritalara, gösterdiği alana giren tam derece enlem ve boylamları
çizilir. Ancak küçük alanları gösteren haritalarda bazen tam derece enlem ve
boylamı harita üzerinde olmayabildiğinden tam derece yerine ara değerlere sahip
enlem ve boylamlar çizilir. Ait olduğu enlem ve boylam dereceleri enlem ve
boylam cetvellerinin üzerinde uygun bir yere yazılır.
Haritanın
içerisinde uygun yerlere yön ölçümünde kullanılmak üzere bir veya daha fazla
pusula gülü konur. Pusula gülü; haritaya yön ölçmek için konan bir yön
cetvelidir.
Haritanın kitabesi
harita ile ilgili bilgilerin verildiği kısımdır. Kitabenin en üstünde haritayı
basan kurumun amblemi bulunur. Bu amblem uluslar arası haritalarda biri ulusal,
biri de uluslar arası olmak üzere iki tanedir. Amblemin altında haritanın genel
olarak ait olduğu bölgenin ismi bulunur. Onun altında ölçeği, derinlik ve
yükseklik ölçü birimi, yapım tekniği, bilgi kaynakları ve notlar bulunur.
Haritada uygun bir yere, genellikle haritanın sağ veya sol üst köşesine konur.
Ancak haritanın kitabe koymaya uygun olmaması halinde kitabe bilgisi harita
çerçevesine ve haritadaki boş yerlere dağınık olarak ta konabilir.
Seyir haritalarında
yüksekliklerin veya derinliklerin belirtilmesinde “metre”, “feet” veya “fathom”
kullanılır. Hangi birimin kullanıldığı haritanın kitabesinde yazılıdır. Eskiden
İngiliz ve bugün Amerikan sisteminde kullanılan “fathom”, bizde eskiden kulaç
olarak belirtilirdi. Fathom 2 yardalık uzunluktur. 1 yarda, 3 feet’dir[2].
Eskiden bizde “ayak” olarak ta söylenen 1 “Foot” da 12 inç’tir. Amerikan
sisteminde pus olarak ta belirtilen “İnç” metrik sistemde ise 2,54 cm olan
uzunluktur.
Haritalarda derinlik
ve yüksekliklerin bu üç farklı şekilde kullanılmasından dolayı farklı harita
kullanan denizcilere yardımcı olmak üzere bazı haritaların enlem cetvellerinin
yanlarında bu birimleri birbirine çeviren cetveller bulunur.
Harita kıyı hatlarını,
kıyılardaki yapıları, kıyılarda ve karanın daha iç kısımlarında denizden
görülebilecek olan unsurları, deniz ve karadaki seyir yardımcılarını, denizdeki
kayalıkları, batık ve derinlikleri, akıntıları ve diğer birçok, güvenli seyir
için gerekli unsurları belirtir. Kullanılan sembol ve işaretler yayımcı
kuruluşun “Sembol ve İşaretler” kitapçıklarında tanımlanır.
Yeryüzündeki bir
noktanın koordinat sistemine göre mevki; üzerinden geçen enlem ve boylam
değerleri ile ifade edilir. Belirli enlem ve boylamlar yeryüzünde sadece tek
bir noktada kesişirler. Bu özellikleri yeryüzündeki bir noktanın yerinin
tanımlanmasında yani mevkiin belirlenmesinde kullanılır.
Örnek:
40 Derece kuzey enlemi
ile 26 derece batı boylamı yeryüzünde sadece tek bir noktada kesişir ve bu
noktanın yeri ( 400 N – 0250 W) şeklinde gösterilir. Bir
mevki tanımlanırken önce enlem sonra boylam belirtilir. Yazarken araya tire (-)
işareti konur veya enlem üstte, boylam altta olacak şekilde alt alta yazılır.
Yeryüzündeki
noktaların mevkilerinin belirtilmesinde sadece derece olarak enlem ve
boylamların belirtilmesi yeterli olmaz. Bir noktanın mevkiin belirtilmesinde
kullanılan Ekvator ve Greenwich’ten olan açısal farkın tam derece olmadığı
durumlarda bunu ifade edebilmek için derecenin alt birimlerine de ihtiyaç
duyulur. Açının alt birimleri dakika ve saniyedir[3]. 1 derece 60 dakika ve 1
dakika da 60 saniyedir.
Derece rakamın üzerine
konan (0) işareti, dakika rakamın üzerine konulan (‘) işareti,
saniye rakamın üzerine konulan (“) işareti ile belirtilir. Yazılırken önce
derece, sonra dakika ve en sonra da saniye yazılır.
Örnek:
Ekvatorun 40 derece,
30 dakika, 30 saniyede kuzeyinde ve sıfır derece boylamının 54 derece, 30
dakika, 30 saniye doğusundaki bir mevki 400 30’ 30” N – 0540 30’ 30” E şeklinde gösterilir.
Şekilde Amerika
Birleşik Devletlerinin New York şehrinin yeryüzündeki yerini işaret etmekte ve
koordinat mevkiini göstermektedir.
New York ; 420 21’ 30” N – 0710 03’ 37” W
Koordinat mevkileri
mutlaka saniyeli olarak belirtilecek diye bir kural yoktur. İstenirse dakikanın
ondalığı şeklinde de belirtilebilir. 1 Dakika 60 saniye olduğundan saniyeli bir
ifadeyi dakikanın ondalığı haline getirirken orantı kullanırız.
Örnek;
360 42’ 54” değerini ondalığa çevirirken doğrudan
saniye değerine bakarız. 60 saniye,1 dakika olduğuna göre 54 saniye kaç dakika
eder. Orantı ile bulunan cevap 0,9’dur.(54x1/60=0,9) Buna göre 36042’54”
değeri de 36042,9’ şeklinde gösterilebilir.
Burada pratik bir
yöntem kullanabilir, ondalıklı bir ifadeyi saniyeliye çevirirken dakikanın
ondalığını “6” ile çarpar, saniyeyi dakikanın
ondalığına çevirirken “6”ya böleriz.
Örnek:
40,5’ saniyeliğe
çevirirken dakikanın ondalığı olan “5”, “6” ile çarpılır ve saniye olarak
yazılır. (40’ 30”)
Örnek:
40’ 24” ondalığa
çevrilirken saniye “6”ya bölünür ve dakikanın ondalığı şeklinde yazılır.
(40,4’)
Saniyeli veya
dakikanın ondalığı şeklinde belirlenmiş koordinat mevkilerinde ±31m. hata
olabilir.[4] Bu neden ile elektronik mevki belirten cihazlarda koordinat mevki
dakikanın bindeliği şeklinde belirtilerek hata ±0,31m’ye kadar düşürülür. Örnek
olarak (40,500’) şeklinde belirtilen dakikada hata en fazla 31 santimetre
olacaktır.
Haritaların
kenarlarında bulunan enlem ve boylam cetvellerinde dakika araları bazen ondalık
bazen de altılık taksimata göre yapılmıştır. Bir değer okunurken buna dikkat
etmelidir. Eğer dakika arası 2’ye, 5’e veya 10’a bölünmüşse ondalık taksimat
kullanıldığından değeri dakikanın ondalığı şeklinde yazarız. 2’ye Bölündüyse
her çizgi arası 0,5 dakika, 5’e bölündüyse 0,2 dakika, 10’a bölündüyse 0,1
dakikadır. Eğer dakika arası 3 veya 6’ya bölünmüşse değeri saniyeli olarak
yazarız. 3’e bölündüyse her çizgi arası 20”, 6’ya bölündüyse 10”dir. Sonra
isteniyorsa saniyeli ifadeyi ondalıklıya, ondalıklıyı da saniyeliye
çevirebiliriz.
Şekilde 10’lu ve 6’lı
taksimatlar gösterilmektedir. 10’lu Taksimat ta çizgi 8. taksimattan geçmekte
olduğundan değer 50,8’dır. Aynı çizgi 6’lı taksimat ta 5. çizginin yani 50”nin
biraz altında olduğundan bunu da yaklaşık 48” yazabiliriz. Eğer yukarıda
öğrendiğimiz gibi 50,8’yı saniyeye çevirirsek bunun da 50’48” (8x6=48”)
olduğunu da bulabiliriz.
Paralel cetvel deniz
seyir haritalarında bir çizginin paralel olarak kaydırılması amacına uygun
olarak özel olarak imal edilmiş bir çizim ve ölçüm aletidir. Bu cetvel
sayesinde haritada bir noktanın enlem ve boylam değerlerinin ölçülmesi, bilinen
enlem veya boylam değerlerinin kestirilmesi, bir istikametin yön değerinin
ölçülmesi veya bir istikamet hattının bir noktaya kaydırılması işlemleri
yapılabilir.
Paralel cetvel
birbirine eşit uzunlukta atkılar ile bağlanmış iki düz cetvelden oluşur. Paralel
kaydırılacak pozisyonda bir tanesi tutamacından bastırılarak sabit tutulan düz
cetvellerden kaydırılacak taraftaki diğeri serbest olarak tutamacından ileri
alınır. Atkıların durumundan dolayı üst parça ile cetvele göre hem ileri hem de
sağa doğru ilerlenebilir. Alt parça ile de hem aşağı hem de sola ilerleme
sağlanabilir. Bu şekilde devam edilerek bir doğrultu paralel olarak haritada
istenilen yere kaydırılabilir.
Alıştırma 1;
Bir deniz haritasında,
paralel cetvelinizi haritanın bir yan kenarına yapışık olarak yerleştirin ve
karşı kenara kadar paralel kaydırın. Cetveliniz karşı kenara paralel kaydığında
bu işlemi birde haritanın alt ve üst kenarları arasında yapınız. Eğer
kaydırmada paralellikte bozulmalar olursa işlemi tekrar ederek becerinizi
geliştirin.
Alıştırma 2;
Paralel cetvelinizi
enlem cetvelini kesecek şekilde bir enlem çizgisi üzerine yerleştirin. Sonra
cetvelinizin kenarı hep aynı enlem çizgisi üzerinde kalacak şekilde usulüne
göre kaydırarak karşı enlem cetveline kadar gidin. Eğer karşı kenara
geldiğinizde cetvelinizin halen aynı enlem çizgisi üzerindeyse işlemi birde
boylam çizgisi üzerinde yapınız. Paralellikte bozulmalar olursa işlemi tekrar
ederek becerinizi geliştirin.
Paralel cetvelinizi haritanın pusula gülü
üzerinde merkezden belirli bir yöne doğru yerleştiriniz. Sonra bu yönü paralel
cetvelinizi usulüne göre kaydırarak uzaktaki belirli bir noktaya kadar
götürünüz. Sonra paralel cetvelin pozisyonunu bozmadan pusula gülüne geri
dönerek bozulma olup olmadığını kontrol ediniz. Bozulma varsa işlemi tekrar
ederek becerinizi geliştirin.
Paralel cetvel kullanımı sırasında dikkat
edilmesi gereken önemli bir husus; kullanılacak paralel cetvelin atkı göbeklerinde aşınma olup olmamasıdır. Eğer atkıları
cetvele bağlayan vida göbeklerinde aşınmalar varsa cetvel sağlıklı çalışmaz. Bu
neden ile bir paralel cetveli kullanmadan önce mutlaka kontrol etmeli, bozukluk
varsa kullanmamalı, kullanmak zorundaysak, paralel cetveli tek enlem ve boylam
çizgisinden kaydırmakla yetinmemeli, biri alt, biri üst enlem, biri sağ, biri
sol boylam olacak şekilde iki farklı enlem ve boylamdan kaydırma yaparak
sağlama yapılmalıdır.
Deniz seyir
haritasında bir yerin koordinat mevkiini ölçmek için ihtiyaç olan ortam bir
gemi veya seyir laboratuarı, ihtiyaç olan malzeme; seyir haritası, paralel
cetvel, kurşun kalem ve silgisi, yazı kâğıdıdır.
● Paralel cetvelin kenarı haritada
koordinat mevki ölçülecek yerin yakınındaki bir enlem çizgisine bitişik
yerleştirilir.
● Paralel cetvel paralelliği
bozulmadan koordinat mevki ölçülecek yerin üzerine kadar kaydırılır.
● Paralel cetvel koordinat mevki
ölçülecek yer üzerindeyken enlem cetveli üzerindeki hizası işaretlenir.
● Enlem cetveli üzerinde işaretlenen
yerin enlemi tam olarak derece, dakika ve saniye veya dakikanın ondalığı olarak
okunur.
● Paralel cetvelin kenarı haritada
koordinat mevkii ölçülecek yerin yakınındaki bir boylam çizgisine bitişik
yerleştirilir.
● Paralel cetvel paralelliğini
bozulmadan koordinat mevki ölçülecek yerin üzerine kaydırılır.
● Paralel cetvel koordinat mevki
ölçülecek yer üzerindeyken boylam cetveli üzerindeki hizası işaretlenir.
● Boylam cetveli üzerinden işaretlenen
yerin boylamı tam olarak derece, dakika ve saniye veya dakikanın ondalığı
olarak okunur.
● Okunan değerler önce enlem sonra
boylam olarak yazılarak ölçülen yerin koordinat mevkii belirlenir.
Uygulamada dikkat edilecek hususlar;
● Paralel cetvel kullanılmadan önce
sağlıklı çalıştığı kontrol edilir.
● Eğer paralel cetvel aynı anda hem
koordinatı okunacak yer hem de enlem veya boylam cetveli üzerine gelmiyorsa
mevkiinin hizasını okumak için paralel cetvel enlem veya boylam cetveli üzerine
usulüne uygun kaydırılır.
● Enlem veya boylam cetvelinden değer
okuma sırasında dakika aralarının kaça bölündüğüne dikkat ediniz. Dakika 10’a
veya 10’un katlarına bölündüyse enlem dakikanın ondalığı olarak, 6 veya
katlarına bölündüyse saniyeli olarak okunmalıdır. Sonra istenirse birbirine
çevrilebilirler.
Marmaris iç
liman çıkışında bulunan Yıldız adasının ucundaki İnce Burun fenerinin koordinat
mevkiini ölçünüz.
Bir yerin koordinat mevkiini deniz
seyir haritasına işlemek; o yerin üzerinde olduğu enlem ve boylamlarının harita
üzerindeki kesim noktasını bulmaktır.
Küresel mevki koyma sistemi (GPS-Global Position System) uydular
aracılığı ile yeryüzündeki bir noktanın mevkiini verebilen bir sistemdir.
Gemilerde bu sistemden yararlanarak mevki koymaya yarayan, bilinen genel ismi
ile “GPS” cihazları bulunmaktadır. Cihaz bir anten aracılığı ile GPS
uydularından aldığı sinyalleri değerlendirerek bulunduğu yerin koordinat
mevkiini hesaplar. Bu değer cihazın ekranından okunur. Gemilerde bu ana
fonksiyonun yanı sıra alınan koordinat değerlerinden yararlanarak birçok seyre
yardımcı bilgiler verebilen GPS cihazları kullanılmaktadır.
Haritaya GPS cihazından alınan veriye göre mevki
konulmasında; verinin elektronik cihazdan alındığını gösteren, bir kutu
içerisindeki hassas kesişmeyi gösteren artı şeklindeki mevki işareti
kullanılır. Bir yayından öğrenilen koordinat mevkilerinin işlenmesinde de aynı
şekil kullanılır Hareketli unsurların koordinat mevkilerinin yanına ayrıca
mevki saati de yazılır.
Bir yerin koordinat
mevkiini deniz seyir haritasına işlemek için ihtiyaç olan ortam; bir gemi veya
seyir laboratuarı, ihtiyaç olan malzeme; seyir haritası, kurşun kalem ve
silgisi, paralel cetveldir.
● Koordinat mevkiinin enlem değerini haritanın yakın
tarafındaki enlem cetveline işaretlenir.
● Koordinat mevkiinin boylam değerleri haritanın yakın
tarafındaki boylam cetveline işaretlenir.
● Paralel cetvelin kenarını yaklaşık mevkiin
yakınındaki enlem çizgisine bitişik yerleştirilir.
● Paralel cetvel usulüne göre kaydırarak enlem
cetvelinde işaretlenen enleme getirilir.
● Cetvelin kenarından yaklaşık olarak mevkiinin
bulunduğu yere kısa bir çizgi çizilir.
● Paralel cetvelin kenarı yaklaşık mevkiin yakınındaki
boylam çizgisi üzerine bitişik yerleştirilir.
● Paralel cetvel usulüne göre paralelliği bozulmadan
kaydırılarak işaretlenen boylama getirilir.
● Paralel cetvel usulüne göre kaydırarak mevkiin enlem
çizgisinin üzerine getirilir.
● Cetvelin kenarı ile yaklaşık mevkiin bulunduğu
yerdeki çizgi kestirecek şekilde bir çizgi daha çizilir.
● Kesişen çizgiler kare içerisine alıp yanına saati
yazılarak geminin koordinat mevkiini belirlenir.
Uygulamada dikkat edilecek hususlar;
● Enlem ve boylam cetvellerine işaretleme yapılırken
dakika aralarının kaça bölündüğüne dikkat edilir. Gerekirse çevrim yapılır.
● Haritanın alt ve üst kenarları da birer enlem, sağ ve
sol kenarları da birer boylamdır. Hiza alınmasında gerekirse oraları da
kullanılabilir.
● Harita üzerine çizim ve işaretlemeler
pahalı haritaları yıpratmamak için sadece yumuşak uçlu kurşun kalem ve kurşun
kalem silgisi kullanılır.
● Haritadaki küçük mesafelerin gerçekte çok
büyük mesafeleri temsil ettiğinden kalem ucu açık olmalıdır.
05.06.2008 Günü sabahı
“A” gemisi ile Marmaris iç limandan çıkış yaptınız. Saat 0900’da boğaz
çıkışında geminizin GPS cihazından koordinat mevkiinizi 36047,8’N-028015,9’E
olarak okudunuz. Koordinat mevkiinizi haritaya işleyiniz.
Rota; bir geminin denizde
bir noktadan bir diğerine gidiş için haritada üzerinde planlanarak çizilen
yoludur. Rota hattı; bir geminin haritada üzerinde planlanan bir noktadan bir
diğerine gidiş için değiştirmeden takip edeceği açısal yöndür. Rota hattının
çizimi rota üzerindeki bir noktadan ilerlenecek istikametin harita üzerinde
çizgi ile belirtilmesidir.
Coğrafyada yön;
yeryüzündeki bir noktanın yerküreye göre baktığı taraftır. Yeryüzündeki bir
noktanın kuzey kutbuna baktığı taraf yani bu nokta ile kuzey kutbunu
birleştiren doğrunun gösterdiği taraf “kuzey”dir. Bu referans noktanın güney
kutbuna baktığı taraf yani bu nokta ile güney kutbunu birleştiren doğrunun
gösterdiği taraf “güney”dir. Kuzey ve güney tam birbirinin zıt tarafında ve
aynı doğru üzerindedir.
Aldığımız bu referans
noktadan kuzey ve güney taraflarını birleştiren doğruya bir dik çizdiğimizde bu
dikin Güneşin doğduğu taraf “doğu”, Güneşin battığı taraf ise “batı”dır. Kuzey,
güney, doğu ve batı ana yönlerdir. Bunların aralarında ara ve tali yönler
bulunmaktadır. Ara yönlerin isimleri aralarında bulunduğu ana yönlerin kutup
ismi öne gelecek şeklinde birleştirilmesi ile elde edilir. Kuzey ile batı’nın
arasındaki yön “kuzeybatı”, kuzey ile doğunun arasındaki yön “kuzeydoğu”, güney
ile batının arasındaki yön “güneybatı”, güney ile doğu arasındaki yön
“güneydoğu” olarak isimlendirilir.
Ara yönlerin
aralarındaki yönler de tali yönler olarak adlandırılır. Arasında bulunduğu
yönlerin önce ana yönünün belirtilmesi şeklinde birleşik olarak isimlendirilir.
Örnek; kuzey ile kuzey batının arasındaki tali yön kuzey-kuzeybatıdır.
Yönlerin
belirtilmesinde normal olarak Türkçe isimler kullanılırken kısaltmalarda bu
yönlerin İngilizce karşılıklarının baş harfleri kullanılır. Bizde bu yaygın
kullanıma uygun olarak kısaltmalarda kuzey yerine İngilizce karşılığı olan
“North”un baş harfi “N”yi, güney yerine İngilizce karşılığı olan “South”un baş
harfi “S”yi, batı yerine İngilizce karşılığı olan “West”ın baş harfi “W”yi,
doğu yerine İngilizce karşılığı olan “East”in baş harfi “E”yi kullanacağız.
Tabloda ana, ara ve
tali yönlerin açısal yön karşılıkları verilmiştir.
|
Ana
|
Kuzey
|
N
|
000,0
|
|
Tali
|
Kuzey kuzey doğu
|
NNE
|
022,5
|
|
Ara
|
Kuzeydoğu
|
NE
|
045,0
|
|
Tali
|
Doğu kuzey doğu
|
ENE
|
067,5
|
|
Ana
|
Doğu
|
E
|
090,0
|
|
Tali
|
Doğu güney doğu
|
ESE
|
112,5
|
|
Ara
|
Güneydoğu
|
SE
|
135,0
|
|
Tali
|
Güney güney doğu
|
SSE
|
157,5
|
|
Ana
|
Güney
|
S
|
180,0
|
|
Tali
|
Güney güney batı
|
SSW
|
202,5
|
|
Ara
|
Güneybatı
|
SW
|
225,0
|
|
Tali
|
Batı güney batı
|
WSW
|
247,5
|
|
Ana
|
Batı
|
W
|
270,0
|
|
Tali
|
Batı kuzey batı
|
WNW
|
292,5
|
|
Ara
|
Kuzeybatı
|
NW
|
315,0
|
|
Tali
|
Kuzey kuzey batı
|
NNW
|
337,5
|
Denizde görülen
bir unsurun kabaca yerini belirtilmesinde bu yönler yeterli olmakla birlikte,
seyirde çok daha hassas değerlere ihtiyaç bulunmaktadır. Bu neden ile seyirde
açısal yönler kullanılır. Açısal yönlerde referans “kuzey”dir. Kuzey “000”[5]
derecededir. Açısal yönler saat yelkovanı istikametinde artarak 3600
ye kadar devam eder. 3600 ile 0000 dereceleri aynı yönü
yani kuzeyi gösterir.
Tablodaki
İsimlendirilmiş yönlere baktığımızda, bunların arasında 22,50 lik
fark olduğunu görürüz. Yönler daha küçük derecelere göre ayrılıp
isimlendirilmemiştir.
Denizde görülen
bir unsurun kabaca yerini belirtilmesinde; ana, ara ve tali yönlerin yetersiz
olduğu durumlarda bugün çok fazla kullanılmamakla birlikte bu yönlerin tam
aralarını ifade eden 11,250lik
“Kerte” ifadesi kullanılabilir.
Örnek:
5 Kerte sancak
ifadesi; kuzeydoğu ile doğu-kuzeydoğu arasını tanımlamaktadır. (Açısal yön
olarak 5x11,25=56,250)
Örnek:
7 Kerte iskele
ifadesi; batı ile batı-kuzeybatı arasını tanımlamaktadır. (Açısal yön olarak
7x11,25=78,750 360-78,75=281,250)
Hem gözlemde
hem de seyirde kullandığımız pusula veya pusula değer gösterici (Repeater)
kartları, ana, ara, tali, kerte ve açısal yön olarak tüm yönleri gösterir.
Şekilde Gösterilen bir manyetik pusula kartında ana, ara, tali yönler ile
açısal yönlerin hepsini görebiliriz.
Pusula gülü harita
üzerinde haritaya göre gerçek ve manyetik yönleri gösteren dairevi bir
cetveldir. Harita üzerindeki bir noktanın bir başka noktaya göre yönünün
belirlenmesinde kullanılır.
Pusula gülünün dış
tarafında hakiki yönleri, iç tarafında manyetik yönleri gösteren çemberler
bulunmaktadır. Çemberler, 00-3600 arasında
işaretlenmiştir. Hakiki yönleri gösteren dış çemberin 00 değeri
haritaya göre coğrafik kuzeyi, manyetik yönleri gösteren iç çemberin 00
değeri de manyetik kuzeyi göstermektedir.
Harita üzerinde bir
noktadan belirli bir yöne bir çizgi çizilecekse, paralel cetvel haritanın
pusula gülü üzerine gülün merkezinden yön istikametine yerleştirilir ve
pozisyonu bozulmadan belirlenen noktaya kadar paralel kaydırılır. Belirli
noktaya gelindiğinde yön istikametinde çizgi çizilir. Burada dikkat edilmesi
gereken, paralel cetvelin haritanın pusula gülü üzerine sağlıklı
yerleştirilmesidir. Cetvelin sağlıklı yerleştirildiği pusula gülünün tam
tersinde cetvelin gülü kestiği yerdeki derecenin, ölçülen dereceden 1800
farklı olması ile kontrol edilir.
ALIŞTIRMA:
Paralel cetvelinizi, seyir haritanızın pusula gülü üzerine
değişik yönlerde yerleştiriniz ve tersinden kontrol ediniz. Tersinden
okuduğunuz değerin 1800 farklı olduğunu görünüz. Bu alıştırmayı
eliniz alışıncaya kadar tekrar ediniz.
Rota hattı çizmek için
ihtiyaç olan ortam; bir gemi veya seyir laboratuarı, ihtiyaç olan malzeme;
seyir haritası, paralel cetvel, kurşun kalem ve silgisi, yazma kâğıdıdır.
● Geminin rota hattı başlangıç mevkiini haritaya
işleyiniz.
● Paralel cetveli pusula gülünün merkezine geminin
harita üzerinde gideceği açısal yönde yerleştiriniz.
● Paralel cetveli pozisyonu bozulmadan, rota hattı
başlangıç mevkiine kadar kaydırınız.
● Rota hattı başlangıç mevkiinden itibaren harita
üzerinde ilerlenecek yöne doğru rota hattını çiziniz.
Uygulamada dikkat edilecek hususlar;
● Kaydırma hatalarından kaçınmak için pusula gülünün
tek olmadığı haritalarda
ölçümün gemi mevkiine en yakın olandan
yapılmasıdır.
● Cetvelin
pusula gülüne yerleştirilmesinde diğer taraftan 1800 farklı değeri
kestiğine dikkat edilmelidir.
05.06.2008 Günü sabahı
“A” gemisi ile Marmaris iç limandan çıkış yaptınız. Saat 0900’da boğaz
çıkışında geminizin GPS cihazından koordinat mevkiinizi 36047,8’N-028015,9’E
olarak okudunuz ve 1500 yönüne doğru gideceksiniz. Bu mevkiden
geminin rota hattını çiziniz.
4.ROTA BACAĞI ÇİZMEK
Birleşerek geminin bir
limandan bir diğerine giderken kullanacağı yolu oluşturan, başlangıç ve bitiş
noktaları birer rota değişim noktası olan düz hatlara rota bacağı denir. Rota
bacağının üzerine geminin gideceği yönü gösteren bir ok çizilir. Ayrıca bu okun
yanına rota kelimesinin İngilizce karşılığı olan “Course” kelimesinin baş harfi
olan “C” ile birlikte yön değeri yazılır.
Rota
bacağı çizmek için ihtiyaç
olan ortam; bir gemi veya seyir laboratuarı, ihtiyaç
olan malzeme; seyir haritası, paralel cetvel, kurşun kalem ve silgisi, yazma
kağıdıdır.
● Rota bacağının başlangıç noktası haritada
işaretlenir.
● Rota bacağının başlangıç noktasından bir doğru hat
üzerinden ulaşacağı bitiş noktası haritada işaretlenir.
● Paralel cetvel yardımı ile rota bacağının başlangıç
ve bitiş noktaları bir doğru çizgi ile birleştirilir.
● Paralel cetvel pozisyonunu bozulmadan pusula gülünün
üzerine kaydırılarak rota hattının yönü okunur.
● Çizilen rota bacağının üzerine yönü gösteren bir ok
işareti ile yön değeri yazılarak rota bacağı oluşturulur.
Uygulamada dikkat
edilecek hususlar;
● Rota hattının başlangıç ve bitimini paralel cetvel
ile birleştirdikten sonra pozisyonunu bozmayınız.
● Rota hattının başlangıç ve bitim noktalarının birleştirilmesinde
paralel cetvel yetersiz kalırsa daha büyük düz bir cetvel kullanılabilir. Ancak
başka bir cetvel kullanılırsa daha sonra paralel cetvel tekrar hat üzerine
yerleştirilir.,
● Pusula gülünden okumada cetvelin pusulada kestiği her
iki yön değeri arasında 1800 derece olduğuna emin olunur.
● Rota bacağı üzerine değer yazılırken yazılan değer
ile okun gösterdiği genel yönün aynı tarafta olduğuna emin olunur.
05.06.2008 Günü sabahı
“A” gemisi ile Marmaris iç limandan çıkış yaptınız. Saat 0900’da boğaz
çıkışında geminizin GPS cihazından koordinat mevkiinizi 36047,8’N-028015,9’E
olarak okudunuz Geminiz bu noktadan rota değişikliği yapmadan 36044,0’N-028018,6’E
mevkiine gidecektir. Geminizin bu rota bacağını haritaya çiziniz.
Yeryüzü alan
şekillerini bire bir aynı ölçülerde kâğıda geçirilmesi ve bu şekilde
kullanılması olanaksız ve yararsızdır. Bu neden ile haritalar yeryüzü alan
şekillerinin belirli bir ölçekte küçültülerek çizilmesi ile oluşturulurlar.
Ölçek kopyanın aslına göre büyüklüğüdür.
Örnek;
● Aslında 100 m uzunluğundaki bir kıyı 1/1000 ölçekli çiziminde 10 cm olarak çizilir.
● 1/2000 ölçekli bir
çizimde 3 cm olarak çizilen bir
iskele aslında 60 m dir.
Deniz
haritalarının çiziminde kullanılan ölçek; haritanın kitabe kısmında yazılıdır.
Haritalarda kullanılan büyük veya küçük ölçekli ifadesi bayağı kesir olarak ölçeğinin
büyük veya küçüklüğünü belirtmektedir.
1/250000
sayısı, 1/500000 sayısından büyüktür. Bu neden ile 1/250000 ölçekli bir harita
da 1/500000 ölçekli bir haritaya göre daha büyük ölçeklidir. Büyük ölçekli
haritalarda unsurlar daha büyük gösterilir. Bir başka deyişle bu haritalarda
daha fazla teferruat görülebilir.
Deniz
haritalarında 3 değişik ölçek kullanılır.
● Tabi Ölçek:
Kopyanın aslına
göre büyüklük oranının bayağı kesir şeklinde ifade edildiği ölçektir. Haritanın
kitabesinde yazılıdır. Haritanın yan kenarlarını sınırlayan boylam üzerinde
oluşturulan enlem cetveli, tabi ölçeğe göre mesafe ölçümünde kullanılır.
● Grafik Ölçek
Cetvel biçimli
grafik üzerinde mesafe belirten ölçeklere grafik ölçek denir. Portolonlarda[6]
kullanılır ve bu haritaların alt veya üst kenarına yakın uygun bir yere konur.
● Adedi Ölçek
Harita
üzerindeki bir uzunluğun gerçekte sahip olduğu değeri belirten ifadesine adedi
ölçek denir. (Örn: 1 cm = 1 km .) Adedi ölçekte, grafik ölçek gibi haritanın her
yerinde uzunlukların aynı olduğu portolon gibi büyük ölçekli haritalarda
kullanılır.[7]
Yerküreyi kutuplardan
geçecek şekilde ortadan ikiye ayırırsak (basıklık ihmal edilmiştir) bir daire
elde ederiz. Bu dairenin kutuptan kutba her bir yarım çemberi, birer boylamdır.
Şekilde görebilmemiz
için bu çember 100 lik dilimlere, bir başka deyişle, enlemlere
bölünmüştür. Burada gördüğümüz gibi her bir enlemin boylam üzerinde böldüğü
kısımlar, yani enlemlerin yeryüzündeki aralıkları birbirine eşittir.
Deniz seyrinde mesafe
birimi, deniz milidir. Deniz mili; mesafeyi tanımlayan rakamın yanında
İngilizce karşılığının (Notical mile) baş harflerinden oluşan kısaltılmış
şekliyle (nm) kullanılır. 1 deniz mili, aralarında 1 dakikalık (derecenin
1/60’ı) açısal mesafe bulunan enlemlerin arasındaki uzaklıktır. Bir başka
deyişle 1 deniz mili; yer merkezinden 1 dakikalık açının yeryüzündeki yay
uzunluğudur. Yeryüzünün basıklığını göz önüne alırsak 1 deniz milini yer
merkezinden 1 dakikalık açının 450 enleminde yeryüzündeki yay
uzunluğudur diyebiliriz.
Bu tanımdan giderek
enlemler arasında yeryüzündeki en kısa yolu aralarındaki açısal farkı hesap
ederek kolayca bulabiliriz.
Örnek:
30042’N
Enlemi ile 30045’N enlemi arasında 3’lık fark vardır. Yani bu iki
enlem arasında yeryüzünden en kısa mesafe 3 nm’dır.
Örnek:
30042’N
Enlemi ile 30045’S enlemi arasında 3687’lık fark vardır. Yani bu iki
enlem arasındaki yeryüzünden en kısa mesafe 3687 nm’dır.
Denizde mesafe
ölçümünde deniz mili ve onun ast katı olan “gomina” ve “yarda” kullanılır. 1 deniz mili 10 gomina ve
2000 yardadır. Deniz milinin üst katı “fersah” dır (Leage). Bir fersah 3 deniz
mili mesafedir.
Denizde mesafe birimi
olarak metre kullanılmamakla birlikte, karada kilometre kullanılmasından dolayı
mesleği yeni öğrenenlere denizdeki mesafe kavramını daha iyi verebilmek için
metre ve deniz mili arasındaki ilişkiyi açıklamakta yarar vardır.
Dünya’nın çevresi
yaklaşık olarak 40.000km’dir. Yeryüzü kesiti bir daire, bir daire 3600,
her bir derece 60’ olduğuna göre, dünyanın çevresi,
360x60=21600 dakika, yani 21600 deniz milidir. Buna göre, 40.000.000 / 21600
=~1852 metre, yani bir deniz mili 1852 metredir. Ancak Dünyamızın gerçekte tam
bir küre olmamasından dolayı, burada bulduğumuz 1852 m değeri, gemi seyrinde
önemli olmayan bir miktarda ekvatora yaklaştıkça büyür, kutuplara yaklaştıkça
ise küçülür. Bu neden ile deniz milinin standart uzunluğu 480
enlemindeki 1 dakikalık boylam uzunluğu olarak belirtilir.
Genel olarak bir seyir
haritasında mesafe; haritadaki 1 dakikalık açıklık 1 deniz mili olacak şekilde
ölçülür. Ancak seyir haritası olarak kullandığımız Merkator haritalarının yapım
tekniğinden dolayı;
● Boylamlar gerçekte kutuplarda birleşirken Merkator
haritalarında boylamların arası eşittir. Bu neden ile mesafe ölçümleri
haritanın alt ve üst kenarlarını oluşturan boylam cetvelinden değil yan
kenarlarını oluşturan enlem cetvelinden yapılır.
● Enlemleri arası gerçekte eşit olmasına rağmen
Merkator haritalarında kutuplara gittikçe enlemlerin arası açıldığından
ölçümler ölçülecek yerin hizasındaki enlem cetvelinden yapılır.
Mesafe ölçümünde
pergel kullanırız. Ölçülecek mesafe kadar açılan pergelin açıklığının enlem
cetvelinden kaç dakikalık uzunlukta olduğuna bakılır ve böylece kaç deniz mili
olduğu söylenir.
Pergelimizin yeterli
olduğu mesafelerde veya kırık hatların ölçümünde pergelin tek açılışı ile ölçüm
yapılır. Ancak, pergel bacaklarının yeterli olmadığı uzun hatlarda bacakları
belirli miktarda açılmış pergelin tekrar eden ölçüm sayısı ile toplam ölçümü
belirlenir. Şekilde Pergel bacakları yetersiz olduğu için pergel sadece 5
nm’lik açılmış ve tekrar edilen ölçüm yapılmıştır. 4 Kere tekrar edilen ölçüm
sonunda kalan miktar kadar daraltılan pergel yan kenardan ölçülerek tekrar
edilen ölçümlere ilave edilmiştir. (4 x 5) + 2.7 = 22.7 nm
Haritada mesafe ölçmek
için ihtiyaç olan ortam; bir gemi veya seyir laboratuarı, ihtiyaç olan malzeme;
seyir haritası, paralel cetvel, pergel, kurşun kalem ve silgisi, yazma
kağıdıdır.
● Pergelin bir ayağı, arasındaki mesafe ölçülecek olan
noktalardan birinin üzerine, diğer ayağı da diğer nokta üzerine konur.
● Pergelin açıklığı bozulmadan bir ayağı ölçülecek yer
hizasındaki enlem cetvelinin bir tam dakika çizgisi üzerine konur.
● Pergel bozulmadan diğer ayağı ile enlem cetveli alt
veya üst tarafından açıklığı kadar işaretlenir.
● Birinci ayak konulan yer ile işaretlenen yer arası,
dakika ve dakikanın ondalığı olarak sayılarak ölçülür ve mesafe deniz mili ve
gomina cinsinden belirtilir.
Uygulamada dikkat edilecek hususlar;
● Pergel kullanılmadan
önce kontrol edilir. Pergel göbeğindeki gevşeme, hatalı ölçümlere sebep olur.
● Ölçülecek mesafe pergel için kadar fazla veya çok
açılmasını gerektiriyorsa hata yapmamak için uzun mesafe ölçümü yöntemini
uygulanır.
05.06.2008 Günü sabahı
“A” gemisi ile Marmaris iç limandan çıkış yaptınız. Saat 0900’da boğaz
çıkışında geminizin GPS cihazından koordinat mevkiinizi 36047,8’N-028015,9’E
olarak okudunuz Geminiz bu noktadan rota değişikliği yapmadan 36044,0’N-028018,6’E
mevkiine gidecektir. Geminizin bu rota bacağının uzunluğunu ölçünüz.
Sürat; birim zamanda
gidilen yoldur. Denizde sürat; 1 saatte deniz mili olarak gidilen yolu ifade
eder ve “Knot” olarak, kısaca “kts” şeklinde belirtilir.
Sürat, yol ve zaman
arasında “sürat = yol /zaman” şeklinde bir bağlantı vardır. Belirli sürede
alınan yol, gemini sürati, belirli bir yolun alınması için gereken zaman bu
bağlantının matematiksel çözümü ile bulunabilir.
Parakete; gemi
süratini suya göre ölçen bir cihazdır. Eskiden seyir sırasında baş taraftan
denize yüzer bir nesne atılır ve bu nesnenin geminin kıç tarafına gelinceye
kadar geçen süresi kronometre ile tespit edilirdi. Sonra geminin mil cinsinden
boyu, saat cinsinden geçen zamana bölünerek geminin sürati hesaplanırdı.
Daha ileri zamanlarda
gemi süratinin belirlenmesi için basit aletler yapılmıştır. Bunlardan en fazla
kullanılanı bir devir sayıcıya bağlı halat ucundaki yüzer pervanedir. Seyir
sırasında geminin kıç tarafından denize bırakılan pervane hareket sırasında
dönmekte, bağlı olduğu halatı çevirmekte, halatta devir sayıcıyı çalıştırmakta
ve devir sayıcı da devir miktarını vermekteydi. Sonra paraketenin süre ve devir
sayısına göre hazırlanan sürat cetvelinden gemi sürati bulunmaktaydı. Bugün bu
cihazlar yerlerini daha güvenilir elektronik cihazlara bırakmıştır.
Kolay anlaşılabilmesi
amacı ile aşağıda küçük tip teknelerde kullanılan sayısal elektronik bir
parakete anlatılmıştır. Bu paraketeler tasarım şekline göre çeşitli işlevlere
sahip olmakla birlikte genel işlevleri;
● O anki nispi sürati vermek, (Suya göre)
● Cihaz sıfırlandığından itibaren ölçülen en yüksek
nispi sürati vermek,
● Cihaz sıfırlandığından itibaren ortalama nispi sürati
vermektir.
Cihaz bir ana ünite ve
bir de pervane şeklinde veri alıcıya sahiptir. Veri alıcı teknenin altına
yerleştirilir.
Veri alıcının
içerisindeki pervane; teknenin altından akan suyun fazlalık veya azlığına göre
hızlı veya yavaş döner ve buna göre yüksek veya alçak voltajda bir elektrik
akımı üretir. Üretilen bu elektrik kablo ile ana üniteye gönderilir. Ana ünite
bu elektriğe göre sürati belirler ve sayısal olarak ekranında gösterir.
Veri alıcı ünite
yelkenli teknelerde teknenin baş tarafına, pervaneli teknelerde ise kıç
tarafına yerleştirilir.
Bugün gemilerde
kullanılan GPS cihazları ek fonksiyon olarak geminin süratini de
hesaplamaktadır. Hesap yönteminde yol; geminin belirli bir zaman aralığında
değişen iki coğrafik mevkii arasındaki mesafe olduğundan bu cihazın verdiği
sürat hakiki sürat olur. Yukarıda anlatılan cihazda veri geminin altından akan
sudan alındığından o cihazda ölçülen sürat nispi sürattir. Örnek olarak
akıntılı bir yerde demirli olan bir geminin yukarıdaki tip paraketesi, gemi
durduğu halde üzerinde yol varmış gibi gösterecektir. Seyir hesaplarında sürat
kullanılırken bu ayrım göz önünde tutulmalıdır.
Parakete mevkii
geminin bilinen son kesin mevkiinden itibaren aldığı yolun hesaplanarak rota
hattı üzerinde işaretlenmesi ile konulan mevkidir. Parakete mevkii cinsini
gösteren yarım daire içerisine konan bir nokta şeklindeki işaretle gösterilir
ve yanına saati yazılır.
Parakete mevki
konularak yapılan seyre parakete seyri denir. Bu seyri genelde aşağıdaki
durumlarda yaparız:
● Kesin mevkiin konulamadığı
durumlarda yaklaşık yerimizi belirlemek için,
● Kesin mevki koyma
imkânlarının olmasına rağmen kesin mevkiler arasında daha küçük taksimatlar
halinde yaklaşık yerimizi belirlemek için.
Parakete seyri
ile ilgili en önemli husus güvenirliğinin az olmasıdır. Parakete mevkiin
doğruluğu aşağıdaki şartlara bağlıdır:
● Akıntı, rüzgar, dümenci
hatası, dümen hatası, pusula hatası gibi nedenler ile rota hattından düşmemiş
olmak,
● Akıntı, rüzgâr, makine devri, dalga
gibi nedenler ile geminin süratinde değişiklikler olmaması.
Bu neden ile
parakete seyri çok gerekmedikçe tercih edilmemelidir.
Parakete mevki koymak
için ihtiyaç olan ortam bir gemi veya seyir laboratuarı, ihtiyaç olan malzeme;
seyir haritası, paralel cetvel, pergel, kurşun kalem ve silgisi, yazma
kağıdıdır.
● Geminin rota bacağı çizilir.
● Son kesin mevki zamanı ile parakete mevki konacak
zaman arasında geçen süre, gemi sürati ile çarpılarak alınan yol hesap edilir.
● Pergel son kesin mevkiden parakete mevkiine kadar
alınan yol kadar açılır.
● Pergelin açıklığı bozulmadan bir ayağı son mevki
üzerine konup diğer ayağı ile rota hattını kestirilir.
● Kesişme noktasına yöntemi tanımlayıcı işareti konularak
mevki saati yazılır.
Uygulamada dikkat edilecek hususlar;
● İşaret koymada kullanılacak pergellerin kalem uçlu
olması haritanın yıpranmasını engelleyeceğinden tercih edilmelidir.
● Çalışma yapmadan önce pergel göbeğinin sağlıklı
çalıştığı kontrol edilmelidir.
05.06.2008 Günü sabahı
“A” gemisi ile Marmaris iç limandan çıkış yaptınız. Saat 0900’da boğaz
çıkışında geminizin GPS cihazından koordinat mevkiinizi 36047,8’N-028015,9’E
olarak okudunuz Geminiz bu noktadan rota değişikliği yapmadan 36044,0’N-028018,6’E
mevkiine gitmektedir. Geminizin pareketeden alınan ortalama sürati 12kts’dır.
Geminizin saat 0910’daki parekete mevkiini haritaya işleyiniz.
Pusula bize yön
gösteren bir cihazdır. Gemilerde teknik olarak iki çeşit pusula kullanılır.
● Cayro pusula,
● Manyetik pusula
Dünya’nın kütlesel
çekim ve dönüş kuvvetinden yararlanılarak yapılan pusulalara cayro pusula
denir. Bize hakiki yani coğrafik yönü verir. Dünya’nın ve geminin
manyetizmasından etkilenmediği için gemilerde kullanılan manyetik pusulalara
karşı avantajlıdır. Dezavantajı ise devamlı olarak düzenli bir elektrik güç
kaynağına ihtiyacının olmasıdır.
Cayro pusula; cayro
sistemini taşıyan bir dolap ve gereken miktarda pusula değer aktarıcılarından
(Repeater) oluşur. Aktarıcılar; sistemden aldıkları sinyale göre bir kürsü
üzerinde taşıdıkları pusula kartını döndüren ve görevli tarafından yön
okunmasını sağlayan cihazlardır. Genelde dümenci önünde, yeke dairesinde ve
kırlangıçlarda bulunur. Cayro pusula kartları da genelde manyetik pusula
kartlarının benzeri görünümündedir.
Manyetik pusula;
yerkürenin manyetik etkisinden yararlanarak yapılan pusuladır. Yeryüzünün
manyetik kuzeyini gösterir. Kullanımında elektrik gibi bir güç kaynağı
gerektirmez. Gemilerde kullanılan bir diğer pusula olan cayro pusulaya nazaran
en büyük avantajı budur. Dezavantajı ise hakiki değil manyetik kuzeyi
gösterdiğinden kullanabilmek için manyetik pusuladan alınan değerlerde düzeltme
yapılması gerekir.
Gemilerde kullanılan
manyetik pusulalar üç ana kısımdan oluşur. Bunlar:
● Tas,
● Kart,
● Sehpadır.
Manyetik pusulanın
tası; pusula kartına serbest hareket edebilmesi için gereken sürtünmesiz ortamı
sağlayan içerisinde gliserin-saf su karışımı bir sıvı bulunan bir kaptır. Kart
bu sıvı üzerinde serbest yüzerek hareket edebilir. Gliserinin amacı suyun
normal hava sıcaklıklarında donmasının engellenmesidir.
Manyetik pusulanın
kartı mika veya plastikten yapılmış, altında bağlantılı 2 adet mıknatıs çubuğu
taşıyan, üstünde yön isimleri, kerte ve dereceleri işaretlenmiş yazılı bir
karttır. Tam ortasından tasın kart taşıyıcı miline oturtulmuştur. Karta bağlı
mıknatıslar kartın üzerinde işaretlenmiş olan kuzey-güney yönünde
yerleştirilmiştir. Bu şekilde serbest olarak sıvı üzerinde dönebilen kart
yerkürenin manyetik alanı etkisi ile daima manyetik kuzey-güney istikametinde
durur. Bir şekilde başka tarafa dönse bile tekrar sabit yönüne geri döner.
Manyetik pusulanın
sehpası pusula tası ile arizi sapmayı[8] düzeltme küre ve çubuklarını taşıyan
kısımdır. Gemiler özellikle sacdan yapılanlar taşıdıkları demir aksam nedeni
ile pusulanın kartındaki mıknatısları etkiler. Dünyanın manyetik alan gücünden
daha kuvvetli olan bu etki nedeni ile pusula doğruluğunu kaybeder ve göstermesi
gereken yönü göstermez. Bu neden ile geminin sahip olduğu manyetik alanın
pusula üzerindeki etkisini en aza indirmek için pusula sehpasının üzerine
sancak ve iskele taraflara birer tane yumuşak demirden küre ve sehpanın
içerisine belirli düzen ve ayarda çubuk mıknatıs çubuklar konur.
Gemilerde kullanılan
bu manyetik pusulalar “standart pusula” olarak belirtilir. Sacdan
yapılmadığından manyetik alan etkisinin çok düşük ve seyir alanı itibarıyla
hatanın ihmal edilebilir derecede olduğu gezi ve spor teknelerinde basit
manyetik pusulalar kullanılır. Bunların üzerinde de basit manyetizma ayar
çubukları vardır. Yatlarda elektronik pusula olarak geçen pusulalarda;
üzerindeki elektrikli bobinler ile manyetizmanın oluşturulduğu bir çeşit
manyetik pusulalardır.
Bildiğimiz gibi kerte
11,250 lik bir açısal aralığı ifade etmektedir. Eskiden yönlerin
belirtilmesinde “kerte” çok kullanılmaktaydı.
“3 kerte sancakta bir fener” veya
“fenerin 1 kerte iskelesinde bir gemi” gibi. Kerteriz kelimesi buradan
gelmektedir. Kerteriz almak; hiza almak, kerteriz değerini ölçmek ise bir
unsurun gemiye göre kaç kerte ne tarafta olduğunu belirtmektir. Ancak bugün
daha hassas işlemler kullanıldığından yön kerte ile değil doğrudan açı ile
ifade edilmektedir.
Gemide bir nesnenin
kerterizini almak için pusula hedefesini kullanırız. Pusula hedefesi pusulanın
üzerine konularak denizdeki, karadaki ve hatta gökyüzündeki bir nesnenin
hizasını ölçmekte kullanılan bir alettir.
Pusula hedefesi çember
biçiminde olup karşılıklı olarak iki kenarında hiza almamıza yarayan parçaları
vardır. Bu iki parçayı hizasını almak istediğimiz nesne ile aynı hizaya
getiririz. Aynı hizaya gelince hedefenin aynasından yansıyan pusula kartına
bakarak, bu hizanın pusulaya göre kaç derecede olduğunu okuruz. Ölçülen bu yön
değeri hedefin pusula kerterizidir.
Nispi kerteriz; bir
geminin çevresindeki bir unsurun, geminin pruvasına göre açısal yönüdür.
Geminin pruvası “0” olarak alınır ve nispi kerteriz “0”dan saat yelkovanı
istikametinde “360” dereceye kadar olan açısal yön ile ifade edilir.
Gemilerde sancak ve
iskele kırlangıçlarda cayro pusula değer aktarıcıları (Repeater) bulunur.
Pusula kerterizleri buradan alınır. Ancak eskiden cayro pusulanın bulunmadığı
zamanlarda dümenci önünde bulunan standart manyetik pusulanın haricinde seyire
yardımcı olarak kırlangıçlara kör hedefeler konurdu. Kör hedefe; kırlangıçlarda
bir sehpa üzerinde bulunan, geminin pruvasını “0” olarak gösteren ve “0”dan
saat yelkovanı istikametinde “360” dereceye kadar derecelendirilmiş bir sabit
daire üzerine yerleştirilmiş hedefelerdir.
Nispi yön ölçümü buradan yapılırken anında dümenci pusulasından da gemi
pruva değerine bakılır ve alınan nispi kerteriz pusula kerterizine çevrilirdi.
Bugün artık
kırlangıçlara konan cayro pusula değer aktarıcıları sayesinde çevre unsurların
pusula kerterizleri doğrudan alınabildiğinden kırlangıçlara kör hedefe
konmamaktadır. Ancak istenirse yine nispi kerteriz, pusulaların dış çerçevesine
konan sabit dairelerden ölçülebilir.
Bugün eskisi gibi
kullanım yeri olmasa bile zaman zaman nispi kerterizlerin pusula kerterizine
çevrilmesine ihtiyaç olmaktadır. Ayrıca seyir zabitinin kavrama kabiliyetinin
geliştirilmesi için buna da gereksinim vardır.
Gemimizden nispi
kerterizi ölçülen bir unsurun pusula kerterizini bulmak için gemimizin pruva
değeri ile diğer unsurun ölçülen nispi kerteriz değeri toplanır.
Örnek;
0400 Pruva
hattında ilerlemekte olan gemimizden nispi 300de kerterizde
edilen bir geminin pusula kerteriz değeri; 40 + 30 = 700dir.
Nispi kerteriz değeri
yukarıda gördüğümüz gibi gemi pruvasından itibaren saat yelkovanı istikametinde
3600ye kadar belirtilebilmesinin yanı sıra, pruvadan itibaren sancak
veya iskele yönünde1800ye kadarda tanımlanabilir. Bu durumda
sancakta kerteriz edilen bir unsurun pusula kerteriz değeri de aynı şekilde
hesaplanır.
Örnek;
0400 Pruva
hattında ilerlemekte olan gemimizden sancak 300de kerterizde
edilen bir geminin pusula kerteriz değeri; 40 + 30 = 700dir.
Nispi olarak kerteriz
edilen bir geminin pusula kerteriz değeri hesaplanırken yapılan toplama
işleminde sonuç 3600nin üzerine çıkarsa, bu değerden 360 çıkartılır.
Örnek;
2700 Pruva
hattında ilerlemekte olan gemimizden nispi 1100de (veya sancak 300de)
kerterizde edilen bir geminin pusula kerteriz değeri; 270 + 110 = 380, 380 – 360 = 0200dir.
İskele tarafta tespit
edilen bir unsurun pusula kerteriz değerini hesaplamak için gemi pruva
değerinden iskele kerteriz değeri çıkartılır.
Örnek;
0800 Pruva
hattında ilerlemekte olan gemimizden iskele 500de kerterizde
edilen bir geminin pusula kerteriz değeri; 80 + 50 = 300dir.
İskele tarafta
kerteriz edilen geminin pusula kerteriz değerini hesaplamak için yapılan
çıkartma işleminde sonuç “-“ çıkarsa, bu değer 360’dan çıkartılır.
Örnek;
0800 Pruva
hattında ilerlemekte olan gemimizden iskele 1500de kerterizde
edilen bir geminin pusula kerteriz değeri; 80 – 150 = -70, 360 – 70 = 2900dir.
İskele tarafta
olmasına rağmen saat yelkovanı istikametinde nispi şekilde tanımlanan bir
geminin pusula kerterizini bulurken önce bu değer iskele taraflı olarak
tanımlanır.
Örnek;
2800 Pruva
hattında ilerlemekte olan gemimizden nispi 2000de kerterizde
edilen bir geminin pusula kerteriz değeri; 360–200=160 (İskele 160), 280 – 160
= 1200dir.
Geminin pruva değeri
iskele tarafta tespit edilen bir unsurun pusula değerinden büyükse; geminin
pruva değerinden diğer unsurun pusula değeri çıkartılır ve başına iskele
ifadesi konur.
Örnek;
0400 Pruva
hattında ilerlemekte olan gemimizden pusula ile 300de kerteriz
edilen gemi bizim 40 – 30 = 100 iskelemizdedir.
Geminin pruva değeri
iskele tarafta tespit edilen bir unsurun pusula değerinden küçükse; diğer
unsurun pusula değeri 3600dan çıkartılarak geminin pruva değeri ile
toplanır ve başına iskele ifadesi konur.
Örnek;
0400 Pruva
hattında ilerlemekte olan gemimizden pusula ile 3300de kerteriz
edilen gemi bizim 360 – 330 = 30, 30 + 40 = 700 iskelemizdedir.
Geminin pruva değeri
sancak tarafta tespit edilen bir unsurun pusula değerinden küçükse; geminin
pruva değeri diğer unsurun pusula değerinden çıkartılır ve başına sancak
ifadesi konur.
Örnek;
0600 Pruva
hattında ilerlemekte olan gemimizden pusula ile 1100de kerteriz
edilen gemi bizim 110 – 60 = 500 sancağımızdadır.
Geminin pruva değeri
sancak tarafta tespit edilen bir unsurun pusula değerinden büyükse; geminin
pruva değeri 360’dan çıkartılarak diğer unsurun pusula değeri ile toplanır ve
başına sancak ifadesi konur.
Örnek;
3100 Pruva
hattında ilerlemekte olan gemimizden pusula ile 600de kerteriz edilen
gemi bizim sancak 360 – 310 = 50, 50 + 60 = 1100mizdedir.
Geminin pruva değeri
tespit edilen bir unsurun pusula değerinden küçükse diğer unsurun pusula
değerinden geminin pruva değeri çıkartılarak nispi şekilde ifade edilir.
Örnek;
0600 Pruva
hattında ilerlemekte olan gemiden pusula ile 1600de kerteriz edilen
geminin nispi kerterizi 160 – 60 = 1000dir.
Geminin pruva değeri
tespit edilen bir unsurun pusula değerinden büyükse geminin pruva değeri
360’dan çıkartılır ve diğer unsurun pusula değeri ile toplanarak nispi şekilde
ifade edilir.
Örnek;
3300 Pruva
hattında ilerlemekte olan gemiden pusula ile 600de kerteriz edilen
geminin nispi kerterizi 360 – 330 = 30, 30 + 60 = 0900dir.
Pusula kerteriz değeri
nispi kerteriz değerinden büyük olan bir unsurun; pusula kerteriz değerinden
nispi kerteriz değeri çıkartılarak gözlemci geminin pruva değeri bulunabilir.
Örnek;
Pusula kerteriz
değeri1300 olan bir unsuru nispi 500de tespit eden
geminin pruva değeri; 130 – 50 = 800dir.
Pusula kerteriz değeri
nispi kerteriz değerinden büyük olan bir unsurun; pusula kerteriz değerinden
nispi kerteriz değeri çıkartılarak elde edilen rakamda 360 dereceden
çıkartılarak gözlemci geminin pruva değeri bulunabilir.
Örnek;
Pusula kerteriz değeri
500 olan bir unsuru nispi 1500de tespit eden geminin
pruva değeri; 50 – 150 = -100, 360 – 100
= 2600dir.
Pusula kerteriz değeri
sancak kerteriz değerinden büyük olan bir unsurun; pusula kerteriz değerinden
sancak kerteriz değeri çıkartılarak gözlemci geminin pruva değeri bulunabilir.
Örnek;
Pusula kerteriz
değeri1300 olan bir unsuru sancak 500de tespit eden
geminin pruva değeri; 130 – 50 = 800dir.
Pusula kerteriz değeri
sancak kerteriz değerinden küçük olan bir unsurun; pusula kerteriz değerinden
sancak kerteriz değeri çıkartılarak elde edilen rakamda 360 dereceden
çıkartılarak gözlemci geminin pruva değeri bulunabilir.
Örnek;
Pusula kerteriz değeri
500 olan bir unsuru sancak 1500de tespit eden geminin
pruva değeri; 50 – 150 = -100, 360 – 100
= 2600dir.
Pusula kerteriz değeri
iskele kerteriz değeri toplanarak gözlemci geminin pruva değeri bulunabilir.
Eğer toplam 360’dan fazla ise 360 çıkartılır.
Örnek;
Pusula kerteriz değeri
0300 olan bir unsuru iskele 500de tespit eden geminin
pruva değeri; 30 + 50 = 800dir.
Örnek;
Pusula kerteriz değeri
3300 olan bir unsuru iskele 500de tespit eden geminin
pruva değeri; 330 + 50 = 380, 380 – 360 = 0200dir.
Pusuladan kerteriz
ölçmek için ihtiyaç olan ortam; bir gemi veya seyir laboratuarı, ihtiyaç olan
malzeme; hedefeli pusula, kurşun kalem ve silgisi, yazma kağıdıdır.
● Kerterizi alınacak unsur
göz ile tespit edilir.
● Pusula hedefesi yönü
ölçülecek unsur hizasına getirilir.
● Hedefe aynasından
gözüken pusula kartından, kerteriz alınan unsurun açısal yönü okunur.
Uygulamada dikkat edilecek hususlar;
Seyir halindeki bir
gemiden yapılan nispi kerteriz
ölçümlerinde pruvanın tam rotayı gösterdiğine, pusula kerteriz ölçümlerinde
geminin gezinmediğine emin olunmalıdır.
05.06.2008 Günü sabahı
“A” gemisi ile Marmaris iç limandan çıkış yaptınız ve 1500 rotasında
ilerlemektesiniz. Gördüğünüz yılancık adası fenerinin pusula kerterizini
alınız.
● Kerterizini alırken.
Kerteriz genelde mevki koyma amacı ile alınır. Ancak
haritaya hakiki kerteriz[9] değerini yani coğrafik yön değerini uygulamamız
gerekirken, pusula ile aldığımız kerteriz değeri[10] pusulada olabilecek sapma
nedeni ile hakiki olmayabilir. Bu neden ile ölçülen pusula kerteriz değerine sapma
düzeltmesi yaparak hakiki kerterize çevirir ve o şekilde kullanırız.
● Dümen
tutarken.
Gideceğimiz yere ulaşmak için hangi yöne gitmemiz
gerektiğini, harita üzerinde buluruz ve pusulamızı kullanarak o yöne gideriz.
Ancak haritadan tespit ettiğimiz değer hakiki kerteriz değeri, pusulada
gördüğümüz değer ise sapmış değer olabilir. Bunun için tespit ettiğimiz hakiki kerteriz
değerine sapma uygulayarak, pusula değerine çevirir ve öyle kullanırız.
Manyetik pusulanın
gösterdiği yön değerini, coğrafik yön değerinden saptıran iki temel unsur
vardır. Bunlar:
● Doğal sapma ve
● Arızi Sapmadır.
Manyetik pusulanın
verdiği değerin kullanılabilmesi için bu iki sapmanın düzeltilmesi gerekir.
Manyetik pusulada
“Doğal sapma”; Dünya manyetizmasının özelliklerinden kaynaklanan gerçek yön
değerindeki sapmadır.
Doğal sapmanın iki
nedeni vardır:
● Manyetik[11] ve coğrafik kutupların farklı yerlerde
olması,
● Yerkürenin manyetizmasının yere ve zamana göre
değişmesi
Belirli yer ve
zamandaki “doğal sapma”, yukarıda belirtilen nedenlerden kaynaklanan sapmaların
toplanması ile yıla ve yere göre değişen bir şekilde meydana gelir. Doğal sapma
değerleri, büyük ölçekli haritaların pusula gülü içerisine yıl, sapma ve
sapmadaki yıllık değişim şeklinde yazılıdır. (Farklı doğal sapma değerlerine
sahip birçok alanı içerdiğinden küçük ölçekli haritaların pusula güllerinde
doğal sapma değerleri yazılı olmaz) Manyetik pusula değerlerine doğal sapma düzeltmesi
yapılırken, harita üzerindeki bu bilgilerden yararlanılır.
Pusula gülü içerisinde
yazılı olan doğal sapma değerini, zamana göre değiştiğinden doğrudan
kullanamayız. Günümüzdeki doğal sapmayı hesap ile buluruz. Bunun için;
● O bölgenin büyük ölçekli bir haritası açılır (Büyük
ölçekli harita, küçük alanları kapsadığından ve haritanın kapsadığı tüm alanda
doğal sapma aynı olduğundan, bu haritaların pusula gülüne, o bölgedeki doğal
sapma yazılır.)
● Pusula gülünden o bölgedeki aşağıdaki bilgiler
alınır,
○ Doğal sapma miktarı
○ Doğal sapmanın tespit edildiği yıl
○ Doğal sapmadaki yıllık değişim
● İçinde bulunduğumuz yıldan, doğal sapmanın tespit
edildiği yıl çıkartılarak, oraya yazılan sapmanın tespit edildiği yıl üzerinden
kaç yıl geçtiği bulunur.
● Geçen yıl miktarı ile yıllık değişim miktarı
çarpılarak, son tespitten sonra toplam ne kadar değişim olduğunu buluruz.
● Doğal sapmanın son tespit değerine, o günden bu güne
kadar olan toplam değişimi uygular ve günümüzde orada ne kadar doğal sapma olduğunu
buluruz.
Burada dikkat edilecek önemli
noktalar,
● Yıllık sapma, “artıyor” veya “azalıyor” şeklinde
belirtilebileceği gibi, (+) veya (-) şeklinde de belirtilebilir. (+) işareti
artıyor, (-) işareti azalıyor şeklinde alınmalıdır. Sapma, gerçek değerden
kaçmadır. Bu neden ile yıllık değişim artıyor şeklindeyse uygulama, sapmayı
büyütecek şekilde, azalıyor şeklindeyse, sapmayı küçültecek şekilde olmalıdır.
● Yıllık sapma “E” veya “W” şeklinde de belirtilebilir.
Doğal sapma ile yıllık sapma aynı işaretli ise sapmanın arttığı, ters işaretli
ise azaldığı anlamındadır.
Örnekler:
a) Doğal sapma 2000 yılında 20 35’ E, yıllık değişim +15’ (veya
15’E) ise 2005 yılında doğal sapma nedir?
2005–2000= 5, 5 x 15’= 75’ , 75’= 10 15’ , (20 35’) + (10
15’ ) = 30 50’ E
b) Doğal sapma 2000 yılında 20 35’ W, yıllık değişim -15’(veya 15’E), 2005 yılında doğal sapma
nedir?
2005–2000= 5, 5 x 15’= 75’ , 75’= 10 15’ , (20 35’ W) - (10 15’ ) = 10 20’ W
Değişim miktarı, sapma
miktarından büyük ve azalıyor şeklindeyse, sapmanın işareti değişir.
Örnek:
c) Doğal sapma 2000 yılında 10 05’ E, yıllık değişim -15’(veya 15’W), 2005 yılında doğal sapma
nedir?
2005–2000= 5, 5 x 15’= 75’ , 75’= 10 15’ , (10 05’ E) - (10 15’ ) = 10’ W
Toplam
değişim, azalma şeklinde sapma kadarsa, sapma ortadan kalkar.
Örnek:
d) Doğal sapma 2000 yılında 10 15’ E, yıllık değişim -15’(veya 15’W), 2005 yılında doğal sapma
nedir?
2005–2000= 5, 5 x 15’= 75’ , 75’= 10 15’ , (10 15’ E) - (10 15’ ) = 0
Gemiler sahip
oldukları demir aksamdan dolayı pruva pupa istikametinde bulundukları yöne göre
değişen bir manyetik alana sahiptir. Bu manyetik alan manyetik pusula üzerinde
belirli bir sapma meydana getirir. Manyetik pusulaların, bulunduğu geminin
manyetik etkisinden kaynaklanarak yapmış olduğu sapmaya “arızi sapma” denir.
Pusulanın arızi
sapması; pusula üzerindeki küre, flander çubuğu ve mıknatıs çubukları ile
uzakyol kaptanı ehliyetli kişiler veya yetkili kuruluşlar tarafından en aza
indirilir. Ancak bu şekilde hem tamamen sıfırlanamadığından hem de geminin
taşıdığı yükler, yaşadığı fırtınalar ve diğer durumlar zamanla bu ayarları
bozduğundan gemilerde ayrıca gerekli hesaplamalar için arızi sapma cetvelleri
kullanılır.
Arızi sapma
cetvellerini hazırlama yetkisi U.Y.Kaptanı ehliyetli kişilere veya
yetkilendirilmiş kuruluşlara aittir. Bu cetvelde; geminin isim ve IMO numarası,
değerlerin alındığı pusula, düzeltmenin yapıldığı tarih, sapma değerleri,
kullanılan yöntem, standart pusuladaki düzeltme unsurlarının durumu,
düzeltmenin yapıldığı mevkii, cetveli hazırlayan kaptanın adı soyadı, ehliyet
derecesi ve imzası bulunur. Özel bir durum olmadıkça cetveller yılda bir
yenilenmek zorundadır. Yük gemilerinde demir yükünün taşınması gibi özel
durumlarda yıl dolmasa bile bu cetvel yenilenir.
EK:1’de bir arızi
cetvel örneği verilmiştir. Bu örnek standart olmamakla birlikte, içeriğindeki
bilgilere sadık kalmak kaydı ile daha kullanışlı olduğu düşünülen bir başka
formatta da hazırlanabilir.
Arizi sapma
cetvelinden sapmayı bulmak için geminin pruva değeri ile girilir, (DİKKAT:
KERTERİZ ALINAN DEĞER İLE DEĞİL!!!) eğriyi kestiği yerden aşağı inilerek sapma
değeri okunur.
Manyetik pusula
değerinden hakiki değere veya bunun tersi olarak hakiki değerden manyetik pusula
değerine çevrim yapmak için iki ayrı yöntem kullanılmaktadır:
Yaygın olarak
kullanılan yöntemde;
C Compass:
Manyetik pusula değerini,
D Deviation:
Arızi sapma değerini,
M Magnetic:
Manyetik değerini,
V Variation:
Doğal sapmadeğerini,
T True:
Hakiki değeri ifade eder.
Bu yöntemde, CDMVT
değerleri yan yana yazılır ve toplama çıkartma işlemi ile bilinmeyen değer
bulunur.
Burada ezberlenecek
olan,
- Pusuladan(C) hakikiye(T), E işaretli sapmalar
toplanır, W işaretli sapmalar çıkartılır,
- Hakikiden(T) pusulaya(C), E işaretli sapmalar
çıkartılır, W işaretli sapmalar toplanır,
Örnek a
Bulunduğumuz yer ve zamanda doğal sapma 120 E, arızi sapma 40
W, pusuladan 3470 de gördüğüm
fener gerçekte kaç derecededir?
|
C
|
D
|
M
|
V
|
T
|
|
3470
|
40 W
|
|
120 E
|
|
|
3470
|
40 W
|
3430
|
120 E
|
3550
|
Örnek b
Bulunduğumuz
yer ve zamanda doğal sapma 120 W, arızi sapma 40 W, pusuladan 3470 de gördüğüm fener
gerçekte kaç derecededir?
|
C
|
D
|
M
|
V
|
T
|
|
3470
|
40 W
|
|
120 W
|
|
|
3470
|
40 W
|
3430
|
120 W
|
3310
|
Örnek c
Haritaya
göre 3550 yönüne gitmem gerekiyor. Bulunduğumuz yer ve zamanda doğal
sapma 120 E, arızi sapma 40 W, manyetik pusuladan kaça gitmem gerekir?
|
C
|
D
|
M
|
V
|
T
|
|
|
40 W
|
|
120 E
|
3550
|
|
3470
|
40 W
|
3430
|
120 E
|
3550
|
Örnek d
Haritaya
göre 3550 yönüne gitmem gerekiyor. Bulunduğumuz yer ve zamanda doğal
sapma 120 E, arızi sapma 40 E, manyetik pusuladan kaça
gitmem gerekir.
|
C
|
D
|
M
|
V
|
T
|
|
|
40 E
|
|
120 E
|
3550
|
|
3390
|
40 E
|
3430
|
120 E
|
3550
|
Örnek e
Haritaya
göre 3550 yönüne gitmem gerekiyor. Bulunduğumuz yer ve zamanda doğal
sapma 120 W, arızi sapma 40 W, manyetik pusuladan kaça gitmem gerekir.
|
C
|
D
|
M
|
V
|
T
|
|
|
40 W
|
|
120 W
|
3550
|
|
3710
|
40 W
|
3670
|
120 W
|
3550
|
Manyetik-hakiki yön
çevriminde “T = C + (E) – (W)” formülü kullanılır.
Bu formülde;
T = True yani hakiki değerini,
C = Compass yani pusula değerini,
(E) = İşareti “E” (East) olan
sapmaların toplamını,
(W) = İşareti “W” (West) olan
sapmaların toplamını ifade etmektedir.
Örnek a:
Bulunduğumuz yer ve
zamanda doğal sapma 120 E, arızi sapma 40 W, pusuladan 3470 de gördüğüm fener
gerçekte kaç derecededir?
T = C + (E) – (W)
T = 347 + (12) – (4) = 355
Örnek b:
Bulunduğumuz yer ve
zamanda doğal sapma 120 E, arızi sapma 40 E, pusuladan 3470 de gördüğüm fener
gerçekte kaç derecededir?
T = C + (E) – (W)
T = 347 + (16) – (0) = 363
Örnek c:
Bulunduğumuz yer ve
zamanda doğal sapma 120 W, arızi sapma 40 W, pusuladan 3470 de gördüğüm fener
gerçekte kaç derecededir?
T = C + (E) – (W)
T = 347 + (0) – (16) = 331
Yukarıdaki örneklerde
pusula değerinden hakiki değere çevrim yaptık ve T = C + (E) – (W) formülünü kullandık. Hakikiden pusulaya
çevrim için yine aynı formülü kullanabileceğimiz gibi, formülü C = T – (E) +
(W) şeklinde de kullanabiliriz.
Örnek d:
Haritaya
göre 3550 yönüne gitmem gerekiyor. Bulunduğumuz yer ve zamanda doğal
sapma 120 E, arızi sapma 40 W, manyetik pusuladan kaça gitmem gerekir?
C = T – (E) + (W) veya T = C + (E) – (W)
C = 355 – (12) + (4) 355 = C + (12) – (4)
C = 347 C
= 347 olur.
Örnek e:
Haritaya göre 3550 yönüne gitmem gerekiyor. Bulunduğumuz yer
ve zamanda
doğal sapma 120 E, arızi sapma 40 E, manyetik pusuladan kaça gitmem gerekir?
C = T – (E) + (W) veya T = C + (E) – (W)
C = 355 – (16) + (0) 355 = C +
(16) – (0)
C = 339 C
= 339
Örnek f:
Haritaya göre 3550 yönüne gitmem gerekiyor. Bulunduğumuz yer
ve zamanda
doğal sapma 120 W, arızi sapma 40 W, manyetik pusuladan kaça gitmem gerekir?
C = T – (E) + (W) veya T = C + (E) – (W)
C = 355 – (0) + (16) 355 = C +
(0) – (16)
C = 371 C
= 371
Bu şekilde manyetik
pusula değerlerini haritaya geçirirken hakikiye çevirebilir veya haritadan
aldığımız değerleri manyetik pusula ile uygulayabilmek için manyetik pusula
değerine çevirebiliriz.
Daha önce
bahsettiğimiz gibi, ahşap veya fiber malzemeden yapılan ve demir aksamın az
olduğu yatlarda, gemi manyetizması ihmal edilebilir olacağından, bu tip
teknelerde arızi düzeltmesi yapılmaz. Ancak doğal sapma düzeltmesi her durumda
gerekir. Bunun için yine aynı formül kullanılacaktır.
Cayro pusulalarda
çalışma sisteminden kaynaklanan sürat, rota ve enlem ayarlarına ihtiyaç vardır.
Bu ayarlar üzerindeki düğmeler ile kullanıcı tarafından yapılır. Ayarları,
elektrik ve mekanik bağlantıları iyi yapılmış sağlıklı bir cayro pusulada hata
olmaz. Gerçek kuzeyi gösterir. Ancak yıpranan pusula veya mekanik bağlantılarından
ile elektrik vasfındaki bozulmalardan dolayı pusulanın gösterdiği değerlerde
hata ortaya çıkabilir.
Cayro pusulanın hatası
varsa bu sabittir. Hatası bilinen bir cayro pusulanın kullanımında bu sabit
hata hesap ile düzeltilerek kullanılır. Ancak istenirse 60ye kadar
olan hatalar pusulanın içerisinde mekanik yöntem ile düzeltilebilir. Hata 60yi
aşarsa servis çağrılmalıdır.
Cayro pusulanın
hatasının tespitinde farklı yöntemler kullanılır. Bunların arasında en kolayı;
boğazlar, limanlar veya benzeri, emniyetli giriş veya geçiş yollarını göstermek
amacı ile konulmuş “Rehber Hat”lardan yararlanarak yapılan hata tespit
yöntemidir.
Rehber hatları yüksek
ve her yönden görünür sabit iki fenerden oluşur. Her iki fener ve fenerin üst
üste göründüğü hat harita üzerinde çizilmiş ve aynı hizada görünme derecesi
belirtilmiştir. Belirtilmese bile bizim ölçme imkanımız vardır. Her iki feneri
aynı hizada gördüğümüzde cayro pusuladan hizasını tespit ederiz. Rehber hattın
haritada verilen değeri ile aldığımız değer arasındaki fark bize cayro pusulamızın
hatasını verir.
Sapma yani
pusula hatası; pusula değerinin hakiki değerden farkıdır.
SAPMA=
HAKİKİ YÖN – PUSULA YÖNÜ ‘dür. (Sapma = T-C )
Örnek:
Bir rehber hattındaki fenerleri aynı
hizada gördüğümüzde, cayro pusulamızla aldığımız hiza 2730 ‘dir.
Rehber hattı, haritada 2700 olarak gösterilmiştir. Bu durumda cayro
hatası yani sapma = hakiki yön – pusula yönü = 270 – 273 = -30 veya
(30W)dir. (CDMVT uygulamasında pusula değerinden hakikiye giderken W
işaretli olan sapma değerleri çıkartıldığından)
Cayro
pusula değerini hakikiye çevirirken yine formül yöntemini kullanabiliriz.
Örnek:
Cayro pusulamızın
tespit edilen hatası 30 W’dür veya bir başka ifade ile -30dir.
Cayro pusula ile alınan 2730 hizasının hakiki değeri nedir.
T = C + (E) – (W) T = 273 – 3 = 2700
Pusula
değerini hakikiye çevirmek için ihtiyaç olan ortam; bir gemi veya seyir laboratuarı, ihtiyaç
olan malzeme; pusula, hedefe, bölgenin seyir haritası, geminin arizi sapma
cetveli, kurşun kalem ve silgisi, yazma kağıdıdır.
● Pusuladan bir referansın açısal yönü belirlenir.
● Manyetik pusula için büyük ölçekli haritanın pusula
gülü içerisinde yazılı haritanın yapım zamanındaki doğal sapma değeri, tespit
yılı, yıllık değişim değeri alınır.
● Manyetik pusula için pusula gülünün içinde bulunulan
yıldan, doğal sapma tespit yılı çıkartılarak, arada geçen yıl sayısı bulunur.
● Manyetik pusula için yıllık değişim değeri, arada
geçen yıl sayısı ile çarpılarak arada geçen sürede oluşan toplam sapma bulunur.
● Manyetik pusula için arada geçen sürede oluşan toplam
sapma harita yapım tarihindeki doğal sapmaya uygulayarak günün doğal sapma
değeri bulunur.
● Manyetik pusula için geminin arızi sapma cetvelinden
pruva değeri ile girerek o yönde arızi sapma değerinin ne olduğu bulunur.
● Cayro pusula için bilinen, manyetik pusula için
tespit edilen sapma değerleri çevrimi yapılacak değere tatbik ederek pusula
değeri hakiki açısal değere veya hakiki açısal değer, pusula değerine çevrilir.
İşlem sırasında dikkat
edilecek hususlar;
● Manyetik pusula için farklı doğal sapma değerlerine
sahip bir çok alanı içerdiğinden küçük ölçekli haritaların pusula güllerinde
doğal sapma değerleri yazılı olmaz. Bu neden ile doğal sapmayı öğrenmek için
bölgenin büyük ölçekli bir haritasına bakılır.
● Manyetik pusula için arızi sapma cetveline pruva değeri ile girilir, kerteriz değeri ile değil.
● Manyetik pusula için arızi cetvele giriş hakiki değer olması gerekirken, fark ihmal edilebilir
olduğundan, cetvele pusula değerinden de girilebilir.
● Çevrimin, pusula değerinden
hakikiye veya hakikiden pusula değerine olması, işlemlerde bir değişim meydana
getirmez, aynı yöntem kullanılır.
● Çevrim sonunda çıkan değer
dakikanın ondalığı şeklinde veya saniyeli ise tam sayıya yuvarlama yapılır.
05.06.2008 Günü sabahı
“A” gemisi ile Marmaris iç limandan çıkış yaptınız ve 1500 rotasında
ilerlemektesiniz. Gördüğünüz yılancık adası fenerinin kerterizini manyetik
pusula ile 0820 olarak ölçtünüz. Yılancık ada fenerinin hakiki
kerteriz nedir, hesaplayınız.
02.02.2008 günü M/V “A” gemisi
Marmaris açıklarında seyir yapmaktadır;
1.Gemi saat 0900’da 36042’48”N-028028’24”E
mevkiindedir. Geminin mevkiini harita üzerine işleyiniz ve koordinat
değerlerini ondalıklıya çevirerek cevap kağıdına yazınız.
2.Gemi bu mevkiden kadırga burnu fenerinin kıyısına kadar
gidecektir. Rota bacağını çizin, üzerine değer ve işaretlerini yazın ve tüm
yolun mesafesini bulun.
3.Geminin sürati saatte 12 kts olup saat kaçta kadırga
burnunda olabilir? İşlemleri cevap kağıdında gösteriniz.
4.Saat 0930 geminin parakete mevkiini haritaya
işleyin ve mevkiin koordinat değerlerini dakikanın ondalığı ve saniyeli olarak
cevap kağıdında yazınız. İşlemleri cevap kağıdında gösteriniz.
5.Gemi rota hattı ile pruva hattı aynı durumda seyir
yaparken bu arada sancak 450 de gördüğü A gemisinin hakiki kerterizi
nedir? İşlemleri cevap kağıdında gösteriniz.
6.Rota hattı ile pruva hattı aynı durumda seyir yaparken bu
arada hakiki 2270 de gördüğümüz B gemisinin nispi kerterizi nedir?
İşlemleri cevap kağıdında gösteriniz.
7.Serdümen cayro pusula ile dümen tutmaktadır. Cayro pusula
hatası 20E’dir. Dümenci akıntı veya rüzgâr yokken rota hattında
ilerleyebilmek için dümeni kaçta tutmak zorundadır? İşlemleri cevap kağıdında
gösteriniz.
8.Gemi rota hattı ile pruva hattı aynı durumda seyir
yaparken geminin arizi sapması ve bulunulan yer ve zamanda doğal sapma nedir?
İşlemleri cevap kağıdında gösteriniz.
9.Gemi rota hattı ile pruva hattı aynı durumda seyir
yaparken cayro pusula arıza yaptığından serdümen manyetik pusula ile dümen
tutmaya başlamıştır. Dümenci rota hattında ilerleyebilmek için manyetik pusula
ile kaç derecede dümen tutmalıdır? İşlemleri cevap kağıdında gösteriniz.
10.Gemi rota hattı ile pruva hattı aynı durumda seyir
yaparken saat 0930 da Yılancık adasının hakiki ve manyetik pusula
kerterizleri nedir? İşlemleri cevap kağıdında gösteriniz.
"Yazı, edinilen
yeni bilgi, değişim ve yapılan yorumlar ile tekrar tekrar
güncellenmektedir. Bu neden ile kopyalayıp almak yerine ihtiyacınız olduğunda
tekrar açıp okumanızda yarar bulunmaktadır. Bu yazı her zaman burada
olacaktır."
[1] İzdüşüm yönteminde her zaman
yerküre merkezi referans alınmaz. Bu referans noktası, yer kürenin izdüşümü
alınan yerin tam tersi yüzeyindeki bir nokta da olabilir. Bu tamamen bir teknik
meselesidir ve farklı isimler altında tanımlanır. Biz izdüşüm yöntemini
anlatırken, kolaylık açısından sadece merkezi referans olarak almaktayız.
[2] Feet; İngilizce’de foot
kelimesinin çoğuludur.
[3] Derecenin alt birimleri olan
dakika ve saniye, saatin alt birimleri olan dakika ve saniye ile
karıştırılmamalıdır.
[4] Dünyanın çevresi = 40000000
m
= 3600, 10 = 40000000/360 = 111120 m , 1’ = 111120/60 = 1852 m ,
1”= 1853/60= 30.8 m
[5] Tam daire 360 derece yani üç
basamaklı bir sayı olduğundan, yanlışlıkları engellemek için açısal yönler
söylenirken başa “0” konularak üç basamağa tamamlanır.
[6] Portolon, çok küçük alanların
gösterildiği, çok büyük ölçekli harita. İsmin kaynağı, “PORTOLANDS” 1500
yıllarında Akdeniz’de kullanılan ve deniz haritalarını kapsayan yayın.
[7] Yerkürede gerçekte enlemler
arası eşit olmasına rağmen Merkator haritalarında kuzeye çıktıkça enlemlerin
arası açılır. Bu nedeni ile bu haritalarda mesafe ölçümü ölçüm yerinin
hizasındaki enlem cetvelinden yapılır. Diğer yerlerden yapılan ölçümlerde hata
oluşur. Ancak portolonlar çok büyük ölçekli olduğundan bu haritalarda enlemler
arası mesafe değişimi ihmal edilebilir orandadır.
[8] Arizi sapma: Manyetik
pusulalarda gemi bünyesindeki çelikten kaynaklanan sapma. Sapma gerçekten
uzaklaşmadır.
[9] Hakiki kerteriz: Coğrafik kuzeye
göre alınan kerterizdir.
[10] Pusula kerterizi: Pusuladan
ölçülen kerteriz değeridir. Pusulanın sapması yoksa hakiki kerterize eşit olur.
[11] Manyetik Kuzey
kutbu, Kanada’nın kuzeyinde Parry Kanalı üzerinde, 740 00’ N – 1010 00’ W mevkiinde,
Manyetik Güney kutbu, Antartika Kıtasında, Mertz Buzulu üzerinde, 680
00’ S – 1440 00’ E mevkiindedir.


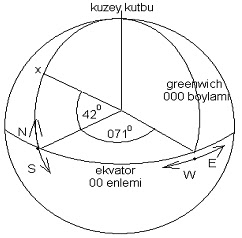






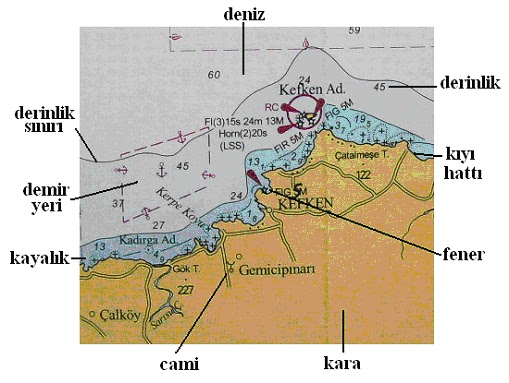
























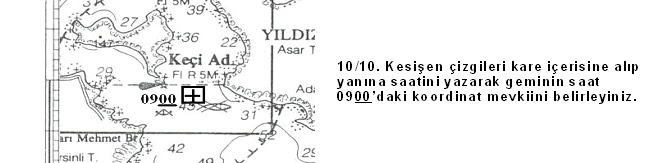
















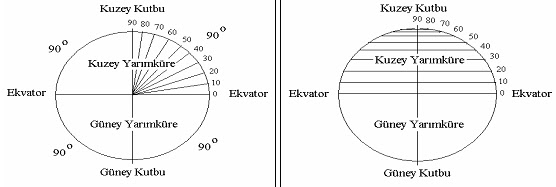



























Konu ne kadar zor görünse de çok güzel anlatmışsınız, emeğinize sağlık.
YanıtlaSilBilgi paylaşımınız için çok teşekkürler.Emeğinize sağlık...
YanıtlaSilGayet anlaşılabilir bir şekilde yapmış olduğunuz ve bu paylaşımı hazırlarken vermiş olduğunuz emeğiniz için teşekkürler.
YanıtlaSil